Distribution-Free Finite-Sample Guarantees and Split Conformal Prediction
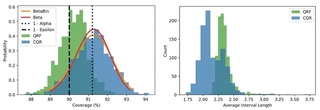 Figure 2
Figure 2
I am a second-year PhD candidate in causal machine learning at the Amsterdam Machine Learning Lab (AMLab), supervised by Sara Magliacane and Herke van Hoof. My PhD is funded by Adyen, a global financial technology company, where I spent a minor portion of my time. My research primarily focuses on causal methods for (nonstationary) time series, although I find myself broadly interested in the intersection of machine learning, statistics and econometrics, with a hint of philosophy.
I graduated with distinction from the University of Oxford with a MSc in Statisticial Science. While at Oxford, I was fortunate to be supervised by Rob Cornish and Arnaud Doucet for my dissertation on the mathematical guarantees of conformal prediction. I also graduated from the University of Groningen with a BSc in Econometrics and Operations Research and a BA in Philosophy of a Specific Discipline (in my case the social sciences), both cum laude.
Before starting my PhD, I spent a short period at ASML as a data analyst for business intelligence, where I optimised business processes for the manufacturing of lithography systems. Afterwards, I moved to a role in AI for healthcare at the Joint Research Centre (JRC) in Italy, an independent research institute of the European Commission. There, I mainly worked on conformal risk control for pulmonary nodule detection and knowledge graph construction using Large Language Models (LLMs).